7 レースカーとCFD
7.1 CFDとは
CFDとはComputational Fluid Dynamicsの略で, 流体の数値シミュレーションのことを指す. 風洞実験と比べてコストがかからず, 形状の最適化やコンセプトの比較がしやすいため, 現代の空力設計においてシミュレーションは欠かせないツールとなっている.
CFDは, 正しく設定されてないと間違えた結果, 傾向に行きついてしまい開発そのものの方向性を見失い兼ねない. また正しくセットアップされていても, 捉えきれない現象, 現実との乖離は出ることがある. そのためF1チームではCFDで結果が良好なデザインのみ風洞でテストするのではなく, 過去に風洞ではCFDと比較してこの流れ場の挙動が違ったからこの形状も風洞に送ってみよう, などという意思決定が取られることもある. しかし学生フォーミュラにおいてこの開発フローを再現することは, 適切な風洞実験を実施するという観点から困難である. そのためCFD, 及び実車走行データをもとに空力開発を進めているチームが多いだろう. またアクセスできる計算資源にも限りがあり, 適切なCFDの設定が困難である場合もある. ここで問題となるのが, 何に重点をおいてシミュレーションを実施するかになってくる.
どの程度の妥協が許され, その妥協は結果にどう影響するか. この点を理解しておけば, ある程度粗いセッティングも有用なデータとなりうる. そのため本稿では, CFDのアルゴリズムや理論, 数学にはあまり深く入らず, レースカーにおけるCFDセッティングの基本、そして正しくないセッティングをしたときに出る結果への影響に焦点を当てていきたい. なおCFDの理論を詳しく勉強したい方は, 梶島先生の「乱流の数値シミュレーション」, またはYoutubeのFluid Mechanics 101をお勧めする.
7.2 CFDの基礎知識
CFDには大きく分けて3種類, DNS, LES, そしてRANSが存在する. この章では各々の特徴を最低限必要な知識に絞り紹介する.
7.2.1 DNS
Direct Numerical Simulationの略. CFDの中では最も精度が高いシミュレーション方法であるが, レースカーにおける空力開発でDNSを用いることはない. その理由は必要とされるメッシュサイズにある. 特に高Re数流れの場合, 要求されるメッシュ数はReに対して指数関数的に増えていく. これは流れの中の最小渦スケール(コロモゴロフスケール)がより小さくなっていくからである. そのためDNSでは現状高Re数での複雑な形状の計算はされず, Re=10e5程度の有限翼のシミュレーションなどが限界である. ただし, 一切のモデル化を行わず(連続体近似など流体力学を構成するうえでの近似はここでは除く)完全にN-S方程式を解くため, ある意味理想的な仮想実験環境を構築することができ, そのために乱流の物理を明らかにするなどの研究用途では盛んに用いられる.
1つ, 余談としてDNSを用いると乱流の瞬時値を正確に予測できるのか?という話がある. 梶島先生の「乱流の流体シミュレーション」によるとできない. これは乱流がカオス現象であり, 完全な初期値がわからない限り, その先の現象を予測できないからである. そのため, DNSを用いたとしても, 得られた速度や圧力のデータを空間, 時間で統計処理したものを扱うことで乱流の特徴を明らかにする, という手法が一般的である.
7.2.2 LES
Large Eddy Simulation, LESはコロモゴロフスケールより大きいとあるスケールを指定し, それ以上大きいスケールはN-S方程式より, そしてそれより小さいスケールの流れはモデル化するという手法である. この手法を用いてもなお必要なメッシュ数は膨大であるが, 近年の計算機の発展に伴い, レースカーに設計にLESでの計算を用いることは不可能ではない. 特に強い渦構造は非定常性が強い場合が多く, LESとRANSによる結果の差が顕著に見られることもある.
7.2.3 RANS
産業界におけるCFDというとおそらく大半がRANS(Reynolds Averaged Navier-Stokes)を指すことが多い. RANSは支配方程式を時間平均する. つまり出てくる量がいわゆる乱流の時間発展によって生じる非定常なノイズを除去した, または時間平滑化された解が出てくる. そして
時間平均したことで発生する速度の変動成分のみで構成される項(移流項の非線形性による)に乱流モデルと呼ばれるモデル化を行い, 変動成分を計算することなく方程式群を閉じる. RANSで要求されるメッシュは乱流モデルの近似による制約が主で, LESなどと比べても必要なメッシュ数が少ない. そのためRANSを使用するためには, ユーザーは乱流モデルを選択しその乱流モデルの近似が成り立つとされる範囲内でメッシュを切る必要がある.
RANSは支配方程式を平均化していることもあり, 非定常現象を見ることに向いていない. URANS (Unsteady RANS)などもソルバーとして選択はできるものの, どの程度の幅で時間平均するのかということを正しく推定するにはエネルギー散逸をスペクトラム評価する必要がある. そのためタイヤのwakeやDRSの過渡応答, 車体の姿勢変化に対する空力的な過渡応答などを評価するにはRANSは向いていない.
RANSの主な目的はメッシュ数を少なくして計算負荷を軽くすることであり, このアプローチの一環として壁関数が使用されることが多い. 高Re数流れになると境界層は薄くなり, 表面からの速度変化の勾配を正確に捉えて剥離の予測をするためにはかなり細かいメッシュを物体表面に用意する必要がある. この問題を解決するために用いられるのが壁関数であり, 粘性長さと粘性速度で無次元化した速度u+と壁面からの高さy+がReに関係なく同じ分布をするという特性を利用して壁面近傍のメッシュを切らずに近似式を用いて正しく速度勾配を予測する. ただし圧力勾配により速度分布が大きな影響を受ける流れ場ではこのアプローチは不向きであり, 壁関数の使用の有無, 壁面近傍のメッシュの精度によって流れの剥離点や剥離の仕方の予測は大きく変わっていく. また近似式にも使用方法があり, 使用するモデルに応じてメッシュの最低限必要な解像度, y+が30以上150未満などと指定されている. 学生フォーミュラの速度域であればy+を5以下に設定して, 壁関数による近似を用いずに直接速度勾配を計算することは現実的である.
7.2.4 乱流モデル
先述した速度の変動成分のみで構成される項(Reynolds応力)の近似モデルのことを乱流モデルという. 近似する方法によって, それぞれ分類分けされているS-A, K-ε, K-ω, K-ω SSTなどがある. 詳しい話は7.3.1節, 及び教科書に任せるが, 乱流モデルの弱点は剝離領域での流れの予測にある. この変動成分項を物理的に解釈すると, 「乱流による細かな変動による時間平均流れへの影響」と解釈できる. そして渦粘性近似と呼ばれる乱流モデルの根幹といえる近似では, この項は粘性項の一部としてスカラー値である粘性係数を用いてモデル化される. ここではつまり, この乱流による細かな変動による影響は, すべての方向に均一に散逸するという仮定がなされている. しかし壁面近傍における乱流の挙動, 境界層に関する流れには異方性があり, この仮定は成り立たない. 結果として乱流エネルギーを過剰に予測してしまい, 剥離や境界層と渦の干渉が正しく予測されないという問題が発生する. 以上はあくまで渦粘性モデルという乱流モデルの根幹にある問題点であって, この上でさらに渦粘性係数をモデル化しているのがいわゆるK-εやK-ωなどである. Kやεの輸送方程式を解く段階でも, 非線形項の挙動に対して近似が行われているため, 二重の仮定がかかっているということに注意されたい.この問題はレースカーの解析においては厄介である. 流れの剥離はタイヤやドライバーのヘルメットでは必ず発生し, その影響は後方に大きな影響を及ぼす. この流れが正しく予測できないということは, 例えばRWの解析結果やラジエータへの空気の流入量などが信頼にかける値になるということである. またサスペンションのアームなどの小さな流れの剥離やその散逸具合も性能予測には十分大きい影響を及ぼす. そんな中でも, 実際RANSに頼ってシミュレーションをしていくしかないのだが, このlimitationを理解しておくと, どの辺りの流れを重点的に実車試験で確認すべきか, 何を信頼して何を信頼しないなどの判断が比較的容易にできるようになる. なお乱流モデルの弱点を補う研究は非常に盛んにおこなわれており, 剥離域で実験と比較してエネルギー散逸が大きく予測される問題には, 剥離域における渦粘性係数を人為的に大きくするなどのチューニングを実験結果と比較しながら行うことがある.
7.2.5 最近の話
近年はGPUの発展もあり, 格子ボルツマン法を用いた大規模計算の例を見るようになった. 精度こそわからないが, F1のモデルなども格子ボルツマン法を用いて解析している例もある. 触ったことがないので紹介だけになるが, GPUの発達に伴い今後主流になる可能性はある. 格子ボルツマン法の利点の1つとしてその並列効率があげられる. うまくプログラムを組むことでCPUと比べてかなり大規模な計算が実施できるようになったり, 高速化できるという利点がある.
またDetached Eddy Simulation(DES)というRANSとLESをハイブリッドさせたシミュレーションは, 120 core程度の計算資源と十分な計算時間があれば現実的に手が届きそうな範囲に位置する. DESに関して詳しく知りたければ, こういう論文やこういう論文をお勧めする. 特にタイヤの後流による影響度を測りたいときは, DESを用いて非定常解析をすることで, より正確な傾向を見ることができる. なお, DESが必ずしもRANSより風洞実験の結果に近い結果になるという確証はない. DESのチューニングにはより多くの計算資源を要するため, 通常はRANSのセッティングを引き継いだ状態で解析を回すことが多い. だがしかし, RANSのモデルのチューニングが必ずしもDESにおいても適切な値とは限らないために, このようなことが発生する. そのためDESの結果を真として捉えるのではなく, RANSではこうなっているがDESではこうなっている. 実際にはDESの流れ場に近いかもしれない, みたいな参考程度とすることをお勧めする. 計算資源にゆとりがあるチームであれば, 用途に応じて様々な解像度のシミュレーションを使い分けるといいだろう.
7.3 CFDのセッティング
RANS, 及び乱流モデルについては前述したとおりであるが, その他CFDのセットアップには多くのパラメータがある. とりあえずデフォルトの状態で使用するだけでは, 不必要な計算資源の浪費や十分でない精度の解析になる可能性があるため, 本章では具体的なCFDのセットアップについて説明する.
7.3.1 乱流モデルとメッシュ
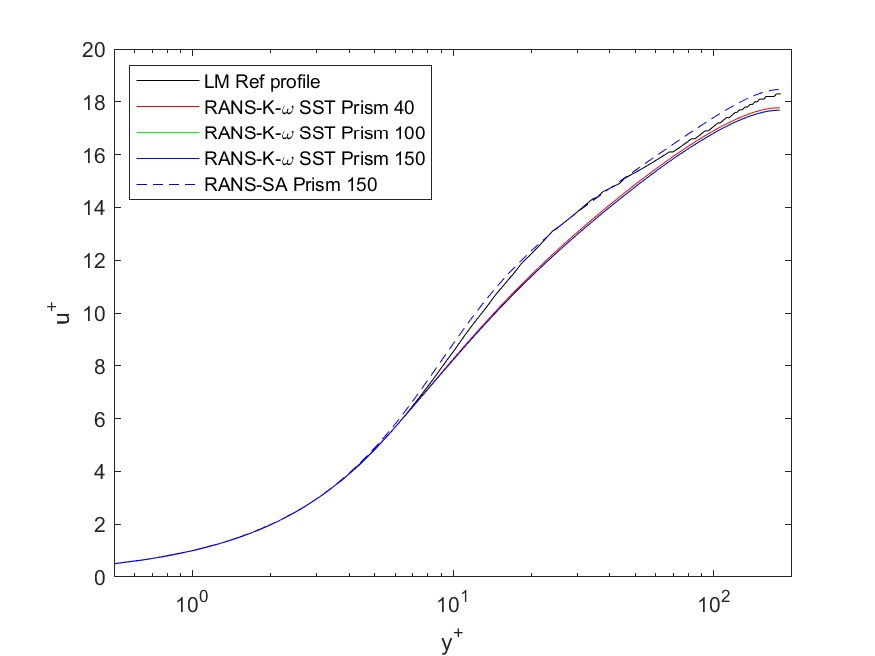
乱流モデルは, K-ω SST一択で問題ない. それ以外のK-εモデルやK-ωモデル, SAモデルも選択はできるだろうが, 基本的にK-εとK-ωのお互いの長所を融合させたモデルがK-ω SSTモデルであり, これ以外を選択する利点があまりない. ただレースカー以外の流れ場, 特に圧力勾配に変化が少ない場合はSAモデルのほうが正しく流れ場を予測できる可能性がある. 例えばチャネル乱流に準ずる流れ場をSAモデルとK-ω SSTモデルで解くと, 境界層の粘性層からLog法則への変化がDNSと比較してK-ω SSTモデルでは下回った結果が出る.
7.3.2 計算領域と境界条件
計算領域は境界条件による影響を流れ場が受けない程度の大きさに設定する必要があり, 簡単にいうと大きければ大きいほどいい. 車の長さを代表長さLとすると, 車前方は5L, 後方は10L, 高さと中心から側面は5L程度を確保しておくと安全だろう. 学術でもOpen Sourceの車のモデルを用いたCFD解析を見かけるが, 普通の車と比べてレースカーの後流, およびupwashはより大きいものとなるため, 市販車より計算領域は大きくする必要がある. 計算領域の流入面積に対しての車体の前方投影面積の比をBlockage ratioというが, Blockage ratioは最低でも5%以下という経験則がある. なお前述した計算領域の設定ではこのBlockage ratioは4%以下になる.
次に与えるべき境界条件を計算領域への影響と共に紹介する. まずInletには速度境界条件を与える. 数学的にはディリクレ境界条件にあたる. このとき, レースカー前方の距離が近すぎると, ノーズからの圧力上昇に影響が出る. 領域底面には滑りなし条件を適応する. またInletと同じ接線速度を地面に与えることで, 車と地面との関係を構築することができる. これによって, FWによって速度に影響が出るまでは境界層が発達せず, 実際の車と同じ状態が再現できる. 車の底面では境界層が発達するため, 車近辺での底面のメッシュは境界層を捉えられるようにする必要がある. 側面には対象境界条件を与える. 中心から側面端までの距離が十分でない場合, 側面が物理的壁として流れ場に影響を与えるため, 例えばタイヤの後流の予測などが少し変化してしまうので十分な幅をとりたい. 上面も同様に対象境界にするとよく, 注意点も側面と同様である. UpwashはDownforceに大きな影響を与えるため, 境界の高さはより性能に敏感だといえる. 最後, Outletには圧力境界条件を与える. これは数学的にはノイマン境界条件にあたる. 速度に関しては1つ前方のセルから移流させるのが一般的だ. この条件は厳密には車体後方の後流によって発生した乱流強度の高い領域のエネルギーが完全に散逸して, 圧力がInlet同様まで回復したあとの流れ場に適応されるべきである. ただしかし, 完全に後流のエネルギーが散逸するのには多くの時間がかかってしまうので, 20L程度の十分に車体から離れた領域にOutletを設けることで, 上流への影響を最小限にしている.
7.3.3 ソルバー
乱流モデルの他にも, どのように各項の微分を計算するか, どの順序でX, Y, Z方向の流体運動方程式を解いていくかを定める必要がある. 学術の分野では近年, 4次やそれ以上の高次の精度を用いた差分法なども研究されているが, 剥離領域では解が振動するなどの課題がありまだレースカーのCFDには実用的ではない(2024年時点). 一般的なソフトウェアでは1次精度か2次精度を選択する程度しかユーザーに選択が残っていないことが多い. 2次の中にも上流のみの情報を用いる風上差分や上流と下流の情報を用いる中心差分があり各項の特性を元に使い分ける必要がある. 具体的な差分の違いや安定性については専門書に任せるとして, ここでは直感的な説明のみを行う.
微分の定義に基づき, 各セルの長さをdxと考え, f(x)をメッシュの中心点にある物理量とすることで各項は計算される. この格子配置を考えるうえで,
スタガード格子やコロケート格子などというキーワードがあるが, これは市販のソフトウェアを使う分には詳しく知る必要がないので専門書に委ねる. ここで対象のセルの値を求めるために, どれだけの前後のセルを用いて微分計算を行うか, 前後両方のセルの値を用いるか, それとも上流の情報のみを用いて計算をするかによって精度と差分の方法が決まってくる. 精度はメッシュのサイズを小さくすることで, どれだけ誤差が小さくなるかということに繋がる. 1次精度であればメッシュサイズを半分にすることで誤差も1/2になり, 2次精度であれば, メッシュサイズを半分にすると誤差は1/4になる. この原理によると, 精度は高ければ高いほどいいように見えるが, 実用的には安定性の問題があるらしい. 次は差分法についてだが, 結論としては移流項のみ上流差分, 粘性項や圧力項には中心差分を適応するといい. 各項の安定性は
ノイマンの安定性解析という方法を用いて判定することができ, 移流項は中心差分よりも風上差分のほうが安定性に優れていることが知られている. 風上差分を用いると, 数値粘性が大きくなってしまい解が鈍るという欠点があるが, RANSにおいては安定性をより重視する上に非定常解析と比較したときに1つ1つのIterationの幅が大きいため, 風上差分を用いるのが一般的だ. そのほかの項に関しては中心差分, 2次精度を用いるとよい.
次は以上の差分法を用いて書き直されたNS方程式をどのような順序で解いていくかという問題に触れよう. ソルバーにはSegregatedとCoupledという2種類が存在する (PISOやSIMPLEなどの速度と圧力方程式のカップリングとは別の話なので注意). 各Iterationごとの計算の流れをざっくりと説明する. Segregatedでは各方向のRANSの運動方程式を圧力項を除いて解く. その後圧力項を連続の式を考慮したうえで求め, その流れ場を用いてKやεなどの乱流モデルの輸送方程式を解く. これに対してCoupledはRANSの運動方程式を圧力項を含め, 全方向同時に求める. そのあとで得られた流れ場よりKやεなどの乱流モデルの輸送方程式を用いる. つまり, 細かく解いていくか, 一気にすべて求めるかというのが大きなコンセプトの違いとなる. Segregatedは実装が比較的容易なうえに, メモリ消費が少ないという点が優れており, Coupled solverは収束が速いという利点がある. RANSでは解の安定性の重要度が高いのでメモリの余裕があれば, Coupled Solverを用いることをお勧めする. 理想とする安定度としては, 最後の100iterationのうちSCLの振動が±0.005以内に収まってほしい.
この安定性を実現させるためにもう1つ大事なのは, ソルバーに倍精度計算も用いるという点だ. プログラミングをする際, ユーザーは1つの数字辺り何ビットを用いてコンピュータに記憶させるかというのを指定する (Pythonなどの最近の言語ではデフォルトが存在しているため, 特に気にしない限りあまり気を遣わなくてもいいが). いわゆるfloatかdoubleのどちらを用いるかという話で, floatでは32bitを用いるので6-7桁, Doubleでは64 bitsを用いるので15桁まで数字が保存できる. ここでの問題はプログラム全体を通じて, 最も大きな数値はいくら程度かということである. 例えば一次元の流れが10m/sから9m/sまで0.01mで減速している領域を考えると, 移流項はざっくりと見積もって9.5*(10-9)/0.01=9500となる. つまりこの場合, Floatを用いた場合の有効数字は小数第2位までとなり, それ以降に続く数字は信頼できない. CFDでは各IterationごとにResidual, 残差が表示されるが残差とは前ステップと現ステップでの数字の差異を正規化したものを指す.この場合の残差を計算すると, 解が収束したとしても保障される数値は小数桁第2位までのため, 0.01/10 = 10^(-3)なので残差は10^(-3)よりも下がることはない. 3次元の流れ場であれば10^(-3)まで残差が収束するなら問題とされるが, 流れ場が複雑になるほど残差は下がりにくい. 以上の理由からCFDのソルバーにはdouble, 倍精度計算を用いることが必須である.
7.3.4 初期条件
計算を回すうえで, 初期条件を決める必要もある. 決めるべき初期条件は, 速度場, 圧力場, そして乱流モデルに関する量になる. 本来最終的に収束した解に初期値依存性はないため, どのような初期条件から始めても問題はないはずであるが, 初期条件は解の収束までの時間に影響を及ぼす.
一番シンプルな初期条件はすべてのセルを流入速度と同じように設定する, またはすべて0の状態から始めるの2つだろう. 自身の経験に基づくと, 境界層近辺の流れを非物理的な速度に設定してしまうと, 速度が下がるまでに時間がかかるため, すべて0の状態から始めるほうが結果として収束までの時間が少なかった. 圧力はReference value, 0で設定しておく.
より高度な初期条件設定としては, 初めの100ステップなどを非粘性ソルバーで解くという方法だ. 非粘性ソルバーでも, 大まかな流れ場を形成するのには役に立つ上に流れ場の成長が速いため, FluentやStarCCM+にはこの機能がデフォルトでついている. ほかにももし似ている形状の流れ場の解が存在する場合, その流れ場を外装するという方法もある. 変更が大きくない場合, このアプローチは非常に有効であり, 収束速度は飛躍的に向上する.
乱流モデルに関する諸量も設定する必要がある. kとε, またはωという2つの変数があるため, 境界条件も2つ定める必要がある. 一般的にはKのnormを速度の主成分で正規化した乱流強度, およびK/ε(=ω)を定めることが多い. k, 乱流強度は平均の流れ場に対しての変動成分の大きさを指す. 風洞実験との比較であれば, この値は1%を下回ることもあるが, 一般的に外を走るレースカーの解析には5%を用いることが多い. これにより, 速度の主成分の5%程度の”揺らぎ”が初期条件に含まれる. この値は層流から乱流への遷移などに影響し, 乱流強度が小さいと遷移点がモデルのsurface上で発生し解が不安定になる. 5%であれば初めから境界層は乱流境界層として発達するため流れ場が安定する. ある意味, 風洞実験におけるTripping wireのような役割を果たしているといえる.
7.3.4 タイヤと地面の粗さモデル
最後に少し発展的な話題にも触れよう. タイヤや地面は決して完全に滑らかなわけではなく, 表面粗さが存在する. そしてこの表面粗さは空力に対して少なくない影響を与えることが知られている. 具体的には表面が粗いほど境界層が厚くなり, タイヤの剥離点の移動や後流の形にも変化がみられる. 地面の粗さは地面近くに渦がある場合に強く影響を与え, 粗い地面の上では渦のエネルギーは境界層によってより散逸しやすくなるため, 結果として渦の寿命が短くなるなどの影響がある. ただし, 現状万能な地面の粗さを再現できるモデルは存在せず, 学術的にも大きな課題となっているため, 風洞実験でのPIVなど, お手本となるデータがない場合は, 特にいじれる場所ではない.
7.4 最後に
学生フォーミュラであっても, 理想的な話をするとCFDの中身を正しく理解したうえで, セッティングを見ることのできる人材がチームに1人はほしい. だがしかし, 多くの場合が設計者が年度初めにCFDを設定して, その設定を使用し続けることが多いと思われる. もちろん様々なCFDの設定を試しながら学習することをお勧めしたいが, 時間, 資源に余裕がない場合は上記のセッティングを活かしてみてほしい.
改訂記録