A.1 翼型とは
翼は主に空力的な目的をもった”板”だと考えている. 例えば空気抵抗を低減したいとき, 同じアスペクト比でも長方形よりも翼形状にするほうが性能が向上したり, 揚力を発生させる際に, 形状を調整し流線の曲率を制御することで, ただの板よりも性能の高いものを設計することができる. 代表的な翼型としてはNACA翼やモータースポーツではMSHD, S1223などがあり, 目的に応じて選定されることが多い. だが, 翼理論を理解すると, 目的に応じた翼は自分で描けるようになる. 自分で描くことで細かいパラメータの調整が可能になるため, 本来その場所に必要な空力性能を意図通りに引き出すことが可能となり, 設計の幅が広がる. よって本章では翼にまつわる流れを詳細に見ていく.
なおここでは主にモータースポーツでの応用に重点を絞るため, 非圧縮の仮定が成り立ち, 翼上での境界層はおおむね乱流のものが説明の対象になる. 層流翼などの層流から乱流への遷移に注目した翼系やクリティカル翼など, 音速域での衝撃波の発生を考慮した翼に関しては自身があまり詳しくないため触れない.
A.2 翼理論概要
翼理論は, 迎え角に対して揚力が線形に応答する領域に注目した理論で, 2Dと3Dに大きく分類される. 特にAoAが小さい領域で, 流れ場に翼しかない場合での性能予測は翼理論と実世界で非常に近い結果が得られることが知られているため, 現象を理解する上でこの理論は非常に役に立つ. 3Dのほうがより複雑に考慮するべきことがあるため, 今回は2Dと3Dに分けて解説していく.
詳細に入る前に, 翼理論はすでに多くの教科書やWebsiteで詳細が説明されている. そのため本ページでは式は省略し, コンセプトのみを解説していく. 理論に関するお勧めしたい教科書やwebsiteを以下に示すが, 日本語の教材でも問題ない.
- MIT: Curvature and aerofoil (website)
- Fundamental of aerodynamics : J Anderson (Textbook)
A.2.1 2D翼(Conventional)
流れ場の中に, 中心線に対して非対称な物体があるとき, その物体の流れは上下で異なってくる. 上下の非対称性によって流れの向きが変化するため, 流れは全体的に見ると上向き, または下向きに曲げられることになる. ここで大事なのが, どのように流れを曲げるか, どの程度流れを曲げるかになってくる. 具体的には「どのように曲げるか」が翼上の圧力分布を決定し, 「どの程度曲げるか」が発生させる揚力の大きさを決める. 以下, それぞれのポイントについて, 物理的な原理を元に見ていく. 以降, 曲率という言葉が度々出てくるが, 曲率が大きい=急カーブ, 曲率が小さい=ゆるやかなカーブを意味する.
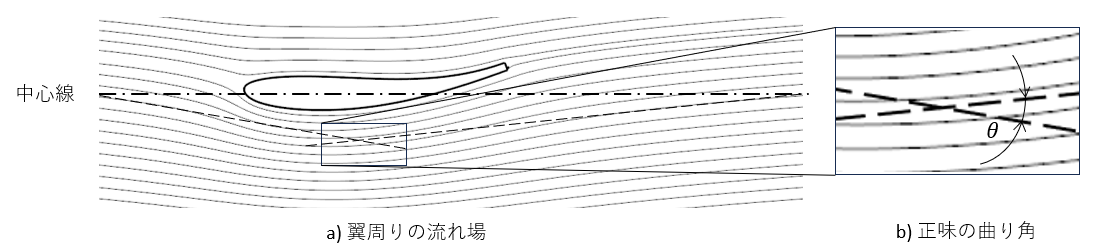
流体力学には, 定常の理想流体に対して流線曲率の定理が存在し, これは流線の曲率と圧力の関係を示したものである. この定理によると, 圧力勾配は流線に直交し, その流線の曲率が大きいほど圧力勾配も大きくなる. 理想流体では粘性を無視しているが, 剥離が起こらない翼周りの流れ場では境界層以外の流れ場に粘性は大きく寄与しないため, この定理は翼周りの流れ場の説明にも適応できる. この定理を直感的に理解する上で便利なのが, 遠心力(向心力)との類似性だ. 流れが曲がるとき, その流れの半径の中心に低圧があり, その低圧部分が力学で言う向心力の役割を果たし流れを曲げていると考えると, どのようなときに圧力が上昇, または低下するかが判断できる. 以下の図b, 流線の図において, 矢印は各点での線の半径の中心を向いており, 物体内側を向いている場合, 物体に近づくほど低圧になるので, その領域では圧力は低下する. 矢印の大きさは曲率の大きさをイメージして描いており, 曲率が大きいほど圧力は低くなる. 翼上面に注目すると, 一度圧力が前縁で上がってから途中で下がり, 最後にまた圧力が上昇する. 下面は前縁付近での負圧が最大となり, それから緩やかに曲率が小さくなっている, つまり圧力が上昇する. この翼の実際の圧力分布, 図Cと比較しても, 曲率と圧力の動きに相関があることが分かる. ここで, 翼上面の圧力が低下する領域が負圧にならない理由は, その前方の圧力が大きく上昇しているからであり, 流線上の圧力は上流の流れの影響を受けるということも見て取れる.
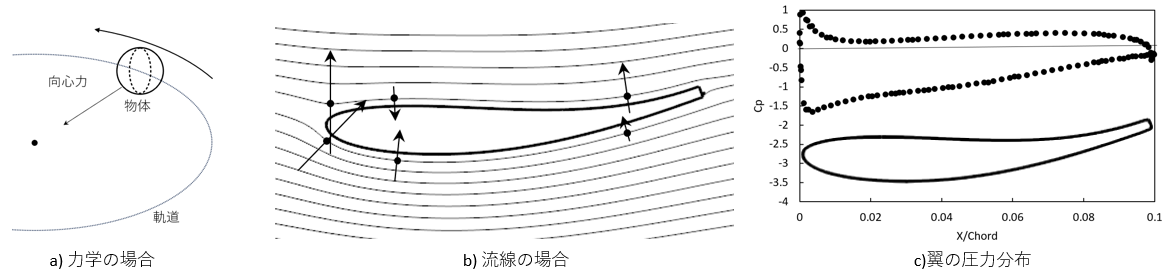
曲率は常に大きい状態を維持すると, 小さな一定半径を持った円を描くことになるので, 流れを曲げる角度によって, どのような曲率を持てるかに制限が出てくる. この話は, 2つ目の「どの程度流れを曲げるか」に繋がる. 流れをたくさん曲げるほど, 曲率を大きくしやすくなり, 流れの曲げる角度が小さいと, 曲率は小さくなる. 結果として流れをたくさん曲げると, 多くの負圧が得られるため, より多くの揚力が得られる. これは形状的にはキャンバーの大きい翼や迎え角の大きい翼に相当する. 理想流体の仮定で, 翼周りの流れ場を実際に計算すると, 流れの曲げ具合と揚力の間には線形関係があることが導かれ, 理想流体の仮定がなりたつ領域, つまり流れが剥離しだすまでの翼性能は2D翼と同等の環境での実験では理論と同等の値を示す. これは大学の学部レベルの実験なので, 読者が物理や工学系の大学出身ならおそらく経験されている人が多いだろう.
次は剥離する寸前まで流線の曲率を大きくしようとした場合, つまり翼の揚力を最大化したいときについて考える. 流体には粘性という摩擦が働く. 粘性は場所によって流速が異なるときに発生し, 空気の場合, 場所による速度勾配のみが粘性の大きさに影響するという近似が成り立つ. 物体の表面上では流れは速度を持つことができない, しかし物体近辺では流れは速度を持つ. よってこの速度0からある一定の速度に至るまで, 物体の近傍には境界層と呼ばれる速度が発達する領域が存在する. 粘性は流体にとっての摩擦なので, 流体を流し続けるにはなんらかのエネルギー, 例えばファンによる強制的な流量供給を与える必要がある. この状態は摩擦とファンによるエネルギー供給が釣り合っている状態だ. これは大域的な議論だけでなく, 局所的な議論にも適用できる. 流体は圧力が高いところから低いところに流れるため, 負の圧力勾配は流体に局所的なエネルギーを供給していると言える. 先ほどの曲率と流れの曲げ具合の話を思い出すと, 曲率を常に大きい状態で保つことはできないため, どこかで必ず流線の曲率は大きい状態から小さい状態に戻ってくる. このときに発生するのが逆圧力勾配になる. これは先ほどの負の圧力勾配とは逆, つまり常に流体からエネルギーを奪う働きをするため, 流体の速度は摩擦+エネルギー減少によって低下していく. イメージは球が坂を下ったあとにもう一度上っているような感覚だ.
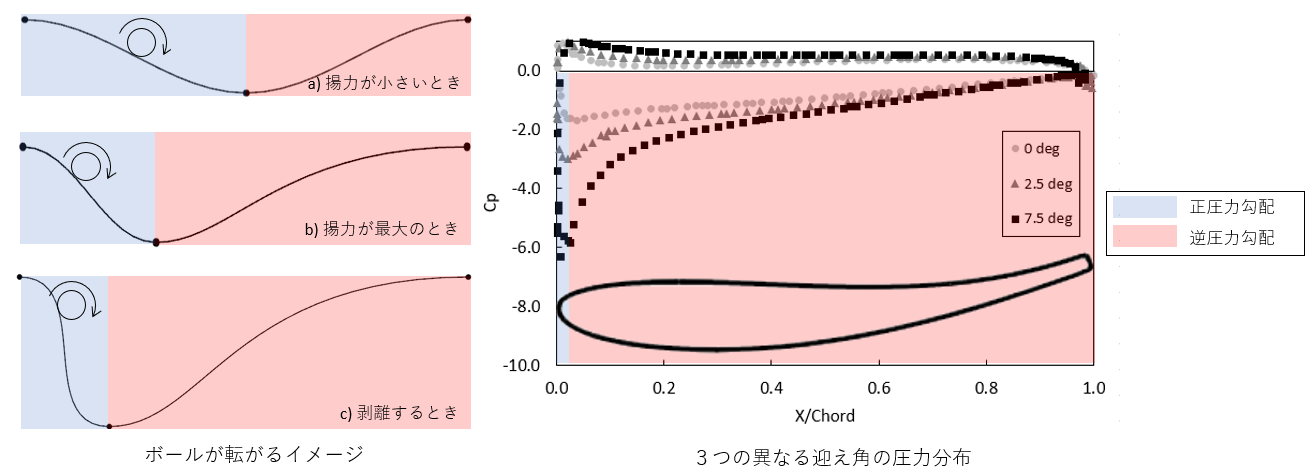
以下に球がスロープを転がるイメージ図と翼上の圧力分布を示す. 圧力分布図のy軸にはCp, 圧力係数を使用しており, 圧力が低いほどこの値は低くなる. このグラフより, 前縁付近の圧力が迎え角に対して大きな反応を示すことが分かる. つまり迎え角を大きくするほど, 前縁での局所的な圧力が低下し, 圧力が最低になったポイントから急激な逆圧力勾配が発生する. 迎え角をあげていくごとに, ボールの図で言うaからcに向かい, ある程度まで行くと流れが剥離する. ただし力学であればcでもエネルギー保存則から問題なく上まで戻ってくる. この違いは粘性による摩擦と動摩擦の違いに起因する. 球に働く力が重力, 垂直抗力, 動摩擦だとすると, 動摩擦係数が速度に対して一定であればその摩擦力も常に一定となるが, 流体の粘性は速度変化によってその大きさが変化するため, 粘性は急激な速度変化を阻害する. つまり流体では坂を下るときに坂道が急すぎると, 本来得られるエネルギーのうち, いくらかが粘性に持っていかれてしまい, エネルギーが不十分な形で急な坂を上り始めることになってしまう.これによって流体は坂道を上りきることができずに, 流れが一部逆流してしまう. これがざっくりとした剥離の原理だ. なおグラフにおける7.5degはこの翼型が剥離を始めるぎりぎりのラインで, Cp=-6はレースカーの設計においてもほとんど見ることがないぐらい低圧な状態だ. 面白いことに, 非粘性流体の場合でも, 流体を急激に曲げようとすると, 流れが剥離する. ただし自分の理解では, 非粘性流体の剥離と粘性流体の剥離は原理が異なるため, 剥離を伴う流れには粘性ソルバーを用いる必要がある.
流れが逆流を始めると, 流れが全体的によりぐちゃぐちゃになり, 乱流強度が大きくなるためエネルギーがより散逸する. さらにこのエネルギー散逸は最初は境界層の中でのみ起こるが, 下流では境界層の外, つまり非粘性流体を仮定していた領域にまで伝播していくため, 形状に沿った流線が得られなくなってしまう. このような問題のため, 剥離領域では流線曲率をした議論が意味をなさなくなり, 流れが制御できないため思うように流れが曲がらず, 翼の性能は下がってしまう. 平均流れ場で見ると, 剥離領域の流れはその場所に停滞し, 渦を巻いている. これによって疑似的にその渦の領域が物体と同様の役割を果たすため, 流線の挙動は想定とは異なるものになる.
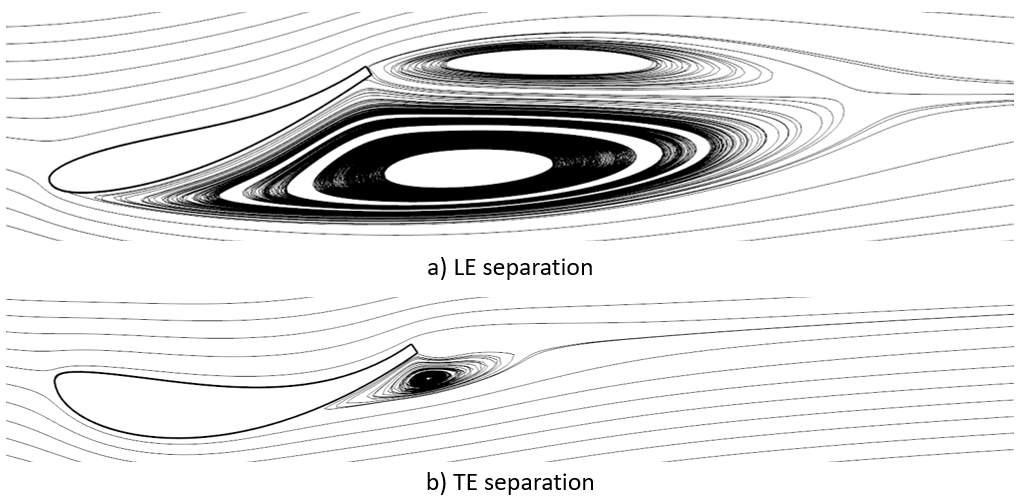
剥離にも翼前方での剥離と翼後方での剥離の2種類がある. 前述の通り, 剥離後の流れは形状には沿わないため, 想定した通りのパフォーマンスを見込むことができない. よって一番よくない剥離の方法は翼前方での剥離になる. 以下の図に実際に翼周りの流れが剥離しているときの流線の図を載せる. 図aでは, 翼の下面の流体が全く形状を沿わず, 剥離領域を回り込むように流線が変動している. これでは翼下面の流れの角度が全く変化しないため, 翼の上面の圧力上昇のみが予想通りに起こり, 下面の負圧は発生しないので翼の性能が大きく低下する. 図bに示した翼後方の剥離も同じように逆圧力勾配に境界層が耐え切れずに発生するが, この際のパフォーマンスの低下比較的なだらかになる. これは, 前方の領域の流れは形状を沿うため, 剥離が起こったとしても小さな曲がり角は確保することができるからだ. 揚力を最大化したい場合, ベストなのは翼の後端で剥離が起こるケースだろう. これはつまり, 翼上での境界層の運動エネルギーをすべて使い切って流れを曲げた状態なので, 揚力を最大化したい場所, 例えばダウンフォースを最大化したい場合のリアウィングの設計思想では剥離位置と後端を一致させるアプローチが適切だろう. 多段翼の原理もここから説明できて, 多段翼ではスロットからより多くの運動エネルギーを境界層に提供することで, もう一度境界層を加速させ, 剥離を防いでいるため, 1つの翼の時と比べてより大きい迎え角をつけることができる.
これまでの議論をまとめると, 翼はその形状により圧力分布や揚力の大きさをコントロールできるが, 剥離が始まるとその通りではない. つまりできるだけ剥離しないような流線をデザインすることが翼設計において重要になってくる. 粘性の性質で議論した通り, 負の圧力勾配を利用するには流れを急激に加速してはならない, つまり大きな圧力勾配の発生は避ける必要がある. 翼にキャンバーをつけると, 翼の前端, leading edge(以下LE)での急激な流線の変化を避けることができるため, 大きな揚力を発生させたいときにはキャンバーをつけることが多い. またキャンバーをつけることで翼の前方での剥離を抑えることができるので, 急激なパフォーマンスの低下を抑えることができる.
A.2.2 2D翼の別の見方(変分法を用いた議論, 2022, Gonzalez)
A1では省略した詳細な計算において, 揚力を決定する際に1つ重要となる仮定をクッタの条件と呼ぶ. これは数ある解の中から, 翼後方のよどみ点が翼の後端に一致するような流れ場を選ぶという仮定で, これによって揚力を1つに定めることができる. 従来, このクッタの条件は1つの粘性モデルだと解釈されてきたが, 例えば後端が二股に別れていたり, 後端が丸いときにはこの条件が適用できない. つまりクッタの条件は万能ではないのだ. よって2023年, 新たに別の方法で翼周りの揚力を理論的に求める手法が提案された. この手法では, N-S方程式をラグランジュ的に考えるところから始まる. これは流体力学でよく議論される, どのように流れ場を見るかという話しのラグランジュ的な視点ではなく, 解析力学におけるオイラーラグランジュ的視点のことを指す. ラグランジュ的に考える最も大きい利点はその系に拘束があった場合に解をより簡単に求めることができるということで, ラグランジュ系では, 最小化すべきコストファンクションが存在する. これは日本語では最小作用の原理と呼ばれており, 今日ではハミルトンのものが一般的だろう. だがしかし, ここで考慮するのはハミルトンの最小作用の原理ではなく, オイラーの最小作用の原理だ. オイラーの最小作用の原理では, とある系に拘束条件, 例えば紐が両端で固定されていたり, 斜面を転がるボールが受ける垂直抗力があった場合, 拘束力があった場合の現象と拘束力がない場合の現象の差分は常に最小化されるということを述べており, 以上より運動方程式における場合の最小化すべきコストファンクションが明確に定義できる. ここでオイラーの最小作用の原理の強いところは, 時間積分した量のみでなく, この関係は各時間ごとに成り立っているというところであり, つまり非定常な流れ場にもこの方法は適用できる.
ここで考えなくてはいけないのは, 流体における拘束力とはなにか. ここで拘束がある状態とは流体内の物体があり流れ場に影響を与えている状態と解釈でき, 理想流体では完全に圧力場に置き換えることができる. よって理想流体では圧力勾配が拘束力となり, これをオイラーの最小作用の原理の式に代入することで, 最小化すべき量が求まる. 理想流体の場合では, この最小化すべき関数は数学的に明確に示すことができるため, その解は解析的に求まる. これを解くと, 理想流体では各流線が曲率を最小化するように収束することが分かり, つまり流れ場は局所的な圧力勾配を与えられた形状という拘束のもとで最小化していると捉えることができる. この結論自体は非常に直感的なものだと思う.
この話は最近学んだ話なので, あまり深い理解はできていないし, 自身があまり解析力学にも精通していないので細かい用語に誤りがあるかもしれない. いつか自分の手を動かしてジューコフスキー翼周りの揚力係数を求めることで, より深く理解できたらと思う.
A.2.3 3D翼
翼が3Dになることで発生する一番大きな違いは, 翼端による影響である. 流れは圧力が高いところから低いところに流れるため, 翼端の上下で圧力差があると, 流れは低圧の方向に引き込まれる結果渦が発生する. これを翼端渦と呼び, この翼端渦による影響が主に2D翼と異なる部分になってくる. なので翼端渦による流れ場の変化について考えていこう.
まずは翼端渦によって生じる速度分布に注目する. 両端の渦により, 上向き, または下向きに追加の速度が付加されるため, 2Dのときと比べて僅かながら翼と流れの角度には差が生じる. これによって翼は形状的な傾き-αの迎え角を受けるため, 揚力の向きが斜め後ろ向きに変化する. このときに揚力の向きのずれによって生じる追加の抵抗を誘導抵抗と呼ぶ. これは翼端渦が強いほど影響が大きくなるため, 特に大きな揚力が発生している状態では2Dと3Dの差が生じやすい. また翼のスパンが大きくなればなるほど渦が翼のスパン中心部に与える影響は小さくなるため, 翼の弦に対してのスパン方向の長さが長いほど, 3次元の翼は効率が向上する.
スパン方向の圧力分布にも差が生じてくる. 翼端渦が発生すると, イメージとしては低圧部分が翼端から漏れ出し, 高圧部分と合流するため, 定常状態では翼端での上下の圧力差はなくなる. この時点でわかることは, 3Dの翼は2Dの翼と比較するとその翼端での圧力差が小さくになることから性能が下がることが分かる. 2Dの翼性能であれば図のようになるが, 実際の3Dの翼は中心から翼端に向けての圧力分布は一定ではなくなる. 数学的に翼端渦の影響を評価することができて, その結果としてその圧力分布を調節することで, 翼端渦による影響を最小限に抑えることができる. 細かい導出は省略するが, 結論としてスパン方向に楕円の圧力分布を持たせることで, L/Dが最大化できることが知られており, この理論に基づいた例としてスパン方向の翼弦を楕円分布させたスピットファイアの翼が挙げられる.
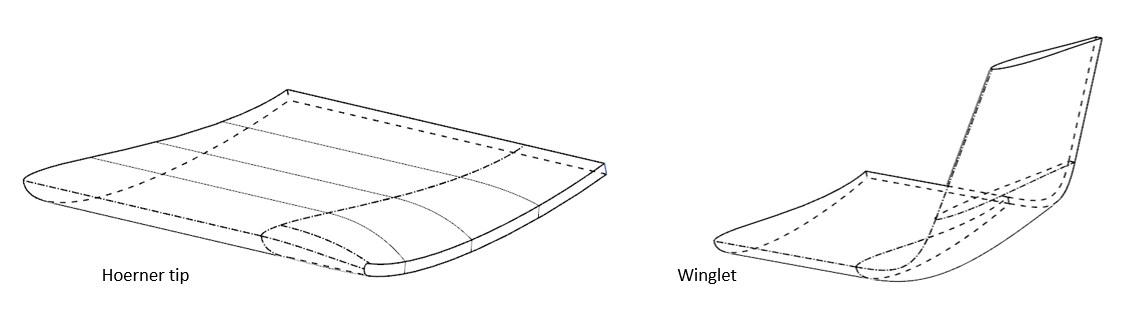
翼端渦への対処法は, スパン方向の圧力分布を調整することだけでなく, ほかにも翼端板をつけたり, 翼端の形状を工夫することでも翼端渦の影響を低減することができる. 翼端板は翼端渦の対処に最もシンプルで効果があるため, レースカーのフロントウィングやリアウィングには必ず付随する. 翼端渦は, 翼の端に蓋をすることで, 低圧部から高圧部への流れの流入を避けることができる. 翼端の端から渦が発生するのは事実だが, 翼端渦と比較すると渦が弱く, さらに迎え角への影響も少なくなるため, 正味の効率が大きく上昇する. 翼端板は大きければ大きいほど2Dの状態に近くなるのでいいが, レースカーの設計では翼端板そのものに空力的な意図を付加させることができるので, レースカーの翼端板は複雑になりやすい. そのほかにも翼端の形状を工夫することで翼端渦による影響を低減することができる. 以下の図に示すように, 航空機によくみられるウィングレットやグライダーなどに用いられているホーナーティップがいい例である. いずれも渦を弱めたり渦をできるだけ遠くで形成するように工夫して, 翼の性能への影響を低減している. 特にホーナーティップはF1の小さな翼の端に多様されており, バージボードが複雑化していた時代についていたアウトウォッシュ用の翼端のほとんどに使用されていた.
翼端渦は地面を活用することでも, その強さを弱めることができる. これは渡り鳥が使う手法として知られるが, 彼らは地面や水面のすれすれを飛ぶことで, 翼端で発生する渦を物理的にブロックし渦を弱めることで, 空気抵抗を削減している. ディフューザの説明に用いられる地面効果のほかに, 分野によってはこれを地面効果と呼ぶこともある. この原理に基づくと, 航空機が海の上を飛ぶときには高度を水面すれすれにするほうが効率がいいのではないか, という質問があってもおかしくないが, 航空機の場合は操縦のインプットに対しての機体の安定性が重要な設計要綱になっており, 地面との距離が近くなるほど, 細かい高度の変化がディフューザなどに用いる地面効果によって揚力に大きな変動を与えてしまうため安定性の確保が困難になるという理由で, 現状ではそのような航空機はないという話を読んだことがある.
A.3 翼理論の応用
これまで色々と翼周りの流れに関する話を議論した. 次は以上を踏まえて少し実用的な話に踏み込む.
まず一番L/Dの高い翼を描く方法を考えてみよう. 改めて翼の形状を見てみると, 前縁付近の低圧側の面は前向きである. つまりこの域で発生させた負圧は, いわゆる推力としての効果を発揮する. もちろん全体でみると空気抵抗は発生するが, この前縁近くで発生する負圧を大きく確保できると, それだけ空気抵抗は少なくなる. よってL/Dを最も高くしたい場合, できるだけ前方付近に負圧が集中するような圧力分布を心掛けるといい. ただしこのような翼には迎え角を大きくしたときに前縁から剥離が始まること, また発生させることのできる揚力が比較的少ないという欠点があるので, どこにでも使用できるわけではないことに注意したい.
次に最も揚力を最大化したい場合の翼を考えてみよう. この場合はできるだけ後ろにキャンバーを付けて圧力勾配をなだらかにするような翼をデザインするといい. 例えばリアウィングのように, リアのエアロのダウンフォースを生み出すメインのエアロデバイスにはこのような翼が用いられることが多い. 圧力勾配がなだらかなため, より大きい迎え角でも剥離せずに多くの負圧を発生させることができるが, 面が後ろ向きの領域でも多くの負圧が発生するため空気抵抗も大きくなるという欠点がある. 例えばディフューザとの機能を連動させたいときに, 意図的に翼の後ろ側にキャンバーを付けることで, リアウィングの効率は犠牲にするがディフューザからの空気の引き抜きの性能を上げて全体の効率を上げる, などの運用方法も考えられる.
A.4 CAD上での描き方
A.4.1 プロファイル
翼型は定量的に曲率をコントロールできるように描くことでが細かい調整ができるようになる. なので自分は以下のようなプロセスで翼のプロファイルを描く. なおLEで一度線を切るかどうかは翼の形による.
- LEのX, Y座標を定義
- Chordを定義
- TEを定義(Chordからの角度は90度である必要はない)
- LEから20, 40%のところに点を定義
- 各点からChordに直角に線を定義
- TEの両端からそれぞれTEに90度で線を定義(場合によっては上面は90度以外でもよい)
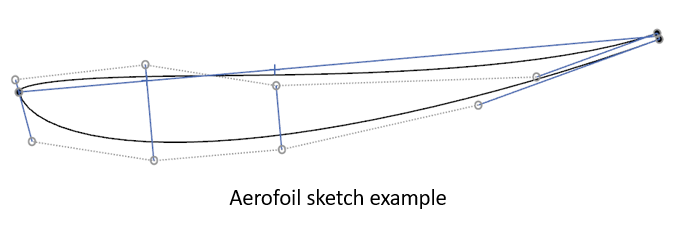
- スプラインで5, 6で定義した線の終点を結び上下, または一本の線を描く. このとき, スプラインが直接通る位置を指定するのではなく, 極を指定するほうが後で調整がしやすい. SOLIDWORKSではDesign Splineがこれにあたる.
- 線の曲率を表示させ, 5, 6で定義した線の長さを調節することで曲率分布を調整
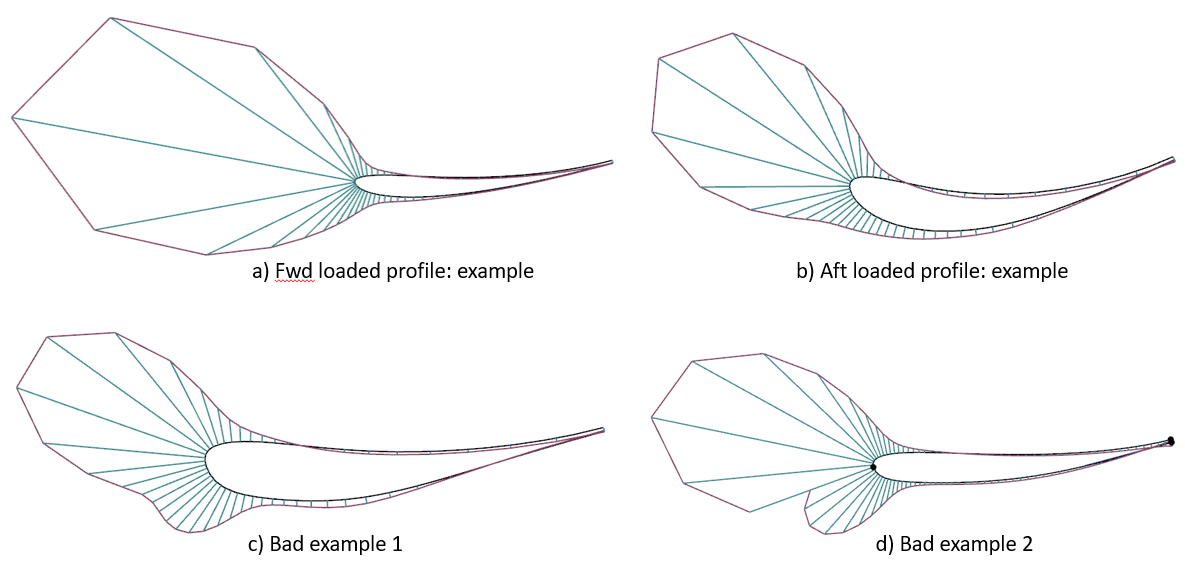
A.3で紹介した翼型, およびよくない例もここで合わせて紹介しておく. aは前方に曲率が集中している. この図はすべて曲率の可視化を同じスケールで描いているため, あまりアグレッシブではないが, よりシャープにすることはできる. 比較的キャンバーは小さいので, 基本的には迎え角を大きくすることで揚力を発生させる必要がある. bは大きな揚力を発生させたいときに用いる翼形状で, RWのメインの翼型はこのようにしておくとドライバーの頭からのダウンウォッシュをうまく活用できる. cとdはよくない例で, 曲率を見ると分かる通り, 曲率分布がスムーズでなく意図が明確でない. このような翼では単にパフォーマンスが下がってしまうだけなので, 既存の翼型を使っている場合も含めて曲率分布を確認することをお勧めする.
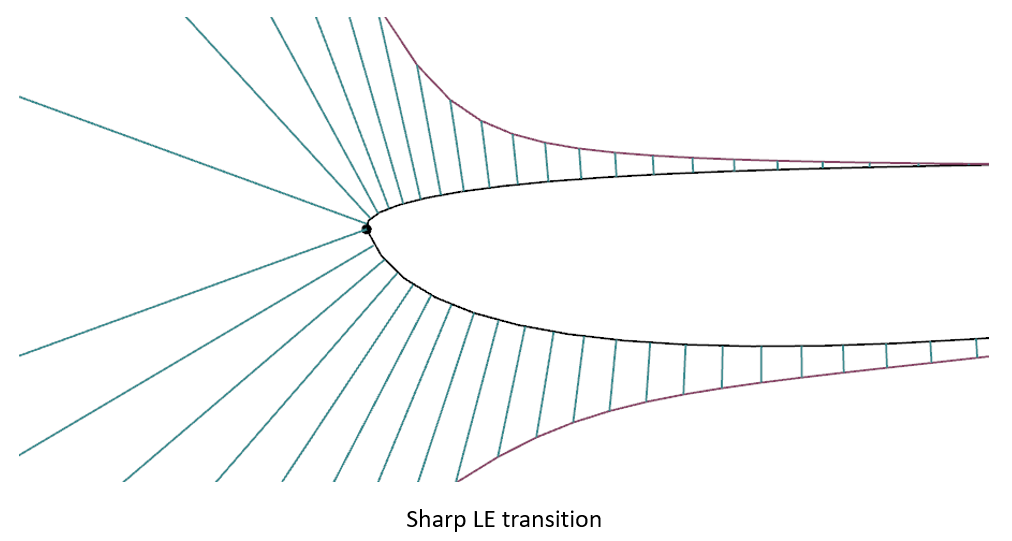
鋭角な前縁が必要な場合, 1つのスプラインで上下を描くのは難しいため, そのときは上下でスプラインを分割し, LEで互いの線が接する, G1の拘束条件を設けるといい. 上下の分割は, 互いの形状の自由度を増やすことに繋がるので, それぞれの調整がしやすくなるというメリットがある一方で, 性能がピーキーになる可能性がある.
A.5 最後に
空力的な意図をもって何かをデザインするときには, 曲率と圧力の関係は翼以外でも剥離していないすべての領域に適用できる話なので, 以上の議論を踏まえてすべての濡れ表面, wet surfaceの曲率に意味を付与することを意識してほしい. サイドをなぜそのように跳ね上げるのか, どうやってリアウィングの翼の曲率分布を決定するか. 形状全てに意味を持たせると, CADで形状を描くことにより時間がかかり, 複雑に, そして職人技に近づいていく. そこまで自分の描いている形状全てに気を遣い物理的な意味を付与することができると, そこがエアロダイナミシストへの第一歩なのではないだろうか, と僕は思う.
改訂記録
28/09/2024: 初版公開 > 同日3Dの翼端の誘導抵抗の説明に訂正